Révisions en TSTI

Exercices de révision physique STI2d

Consignes

Il est FORTEMENT recommandé d’avoir un papier, un stylo et une calculatrice.
Chaque question est un petit problème dont la résolution peut comporter plusieurs étapes.

1 - Énergie vers puissance

La consommation en puissance d’un appareil électrique varie ainsi (axes en t(h) et en P(W)) :

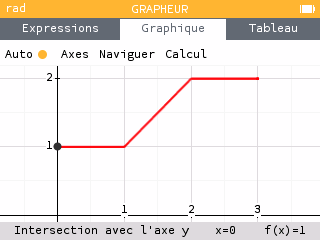
énergie

Calculer en J l’énergie consommée entre t=0 et t=3h.

Aide et solution

Il faut faire l’intégrale (surface sous la courbe) entre 0 et 3. On obtient ensuite l’énergie en W.h puis on convertit en J.

E=1 \times (1-0) + \dfrac{2-1}{2} + 1 \times (2-1) + 2 \times (3-2)=4,5\,W.h

soit

16,2\,kJ

2 - Puissance vers énergie

L’énergie E(J) consommée par un appareil évolue au cours du temps t(s) selon la loi : $E(t)=0,02 \cdot t^2 - 36 \cdot t + 400$ .
Quelle puissance est consommée à l’instant t = 1h30?

Aide et solution

La puissance instantanée est la dérivée de l’énergie (la pente s’il s’agissait d’une courbe). Ici il faut donc dérivée E(t) et on arrive à

p(t)=0,04 \cdot t - 36

donc pour t =1h30 = 5400s on trouve p(5400) = 180W.

3 - Fonctionnement d’une pile

Une pile de capacité Q = 800mA.h, de tension U = 1,5V fonctionne avec les couples $MnO_{2(s)}$ / $MnO(OH)_{(s)}$ et $Zn^{2+}$ / $Zn$ .
On rappelle que : $1\,\mathcal{F} = 96\,500\,C.mol^{-1}$ , $M(Zn)=65,4\,g.mol^{-1}$ , $1\,A.h = 3600\,C$

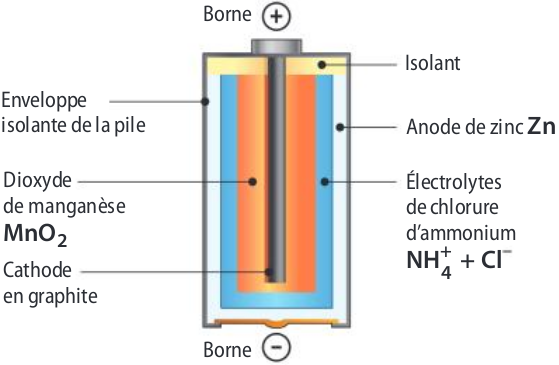
énergie

Établir l’équation bilan de la pile, identifier anode et cathode puis calculer la masse minimale de zinc qui assure la bonne valeur de capacité Q.

Aide et solution

Equations de demi-réaction :
$MnO_2 + H^{+} + 1 e^{-} = MnO(OH) \qquad (\times 2) \quad réduction, cathode, borne +$
$Zn = Zn^{2+} + 2e^{-} \qquad (\times 1) \quad oxydation, anode, borne -$
——————————————————–
$2MnO_2 + 2 H^{+} + Zn \rightarrow 2 MnO(OH) + Zn^{2+}$

2 électrons sont échangés pour 1 atomes de Zn. Le nombre de moles d’électrons nécessaires est

n(e^{-}) = \dfrac{Q}{\mathcal{F}}=\dfrac{0,800 \times 3600}{96\,500} \approx 3,0.10^{-2}\,mol

.
Donc il faut

n(Zn)=\dfrac{n(e^{-})}{2}=1,5.10^{-2}\,mol

de Zn soit

m(Zn)=M(Zn) \times n(Zn) = 0,98\,g

de Zn.

4 - Pile à combustible

La pile utilise les couples $H^{+}$ / $H_2$ et $O_2$ / $H_2O$ et peut fournir $Q = 1250\,mA.h$ . Le dioxygène est l’espèce la plus oxydante.

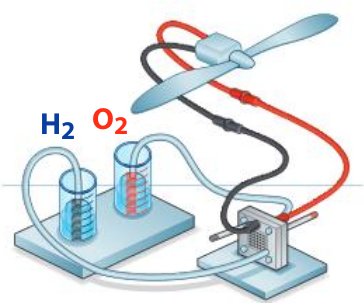
énergie

Dans chaque fonctionnement (charge et décharge), écrire l’équation bilan et identifier anode et cathode ainsi que bornes + et -.
Calculer la durée de fonctionnement $\Delta t$ lors d’une décharge complète qui fournit une intensité I=20mA.

Aide et solution

Les équations de 1/2 réaction sont : $H_2 = 2H^{+} + 2e^{-}$ et $\dfrac{1}{2} \, O_2 + 2H^{+} +2e^{-} = H_2O$

Bilan en décharge : $H_2 + \dfrac{1}{2} \, O_2 \rightarrow H_2O$ , cathode et réduction côté $O_2$ , borne +
Bilan en charge : $H_2O \rightarrow H_2 + \dfrac{1}{2} \, O_2$ , anode et oxydation côté $O_2$ , borne +

Alors en décharge avec $I=20\,mA$ : $\Delta t = \dfrac{Q}{I} = \dfrac{1250}{20} = 62,5\,h$ de fonctionnement en décharge.

5 - Consommation électrique

On considère un moteur asynchrone triphasé 8kW alimenté par $U_{max}=563\,V$ et fournissant $I_{eff}=20\,A$ avec un facteur de puissance k=0,8.

Calculer le rendement $\eta$ de ce moteur.

Aide et solution

P_{elec}=\sqrt{3} \cdot U \cdot I \cdot \cos \varphi = 11\,kW

avec

U=\dfrac{U_{max}}{\sqrt{2}}=400\,V

k=\cos \varphi=0,8

.
Donc le rendement est :

\eta = \dfrac{P_{meca}}{P_{elec}}=\dfrac{8}{11}=73\%

6 - Calculer une puissance active

On considère une tension u(t) (en rouge) et une intensité i(t) (en bleu) consommées par un appareil. Les axes sont en V, A et ms :

énergie

Déterminer le facteur de puissance k puis la puissance active P et la puissance apparente.

Aide et solution

On lit

U_{max}=40\,V

I_{max}=20\,A

donc en divisant par

\sqrt{2}

, les valeurs efficaces sont :

U=28,3\,V

I=14,1\,A

.
On lit également

T=20\,ms

et un décalage temporel

\Delta t=+2\,ms

. (on note que u(t) est en avance sur i(t) et que l’appareil est monophasé). Donc le déphasage de u(t) par rapport à i(t) vaut

\varphi=\dfrac{\Delta t}{T} \times 2\pi= 0,63\,rad

Alors :

P=U \cdot I \cdot \cos \varphi = 28,3 \times 14,1 \times \cos(0,63)=322,4\,W

et le facteur de puissance est

k=\cos \varphi = \cos(0,63)=0,81

.
La puissance apparente est :

S=U \cdot I=28,3 \times 14,1 \approx 400\,W

7 - Ligne HT et transformateur

Soit un transformateur monophasé idéal avec $N_1=70$ spires au primaire et $N_2=420$ spires au secondaire.
La puissance transmise vaut 36W et la tension primaire efficace $U_1=10\,V$ .

Déterminer les valeurs efficaces de la tension secondaire $U_2$ et des intensités $I_1$ et $I_2$ .
Quel est l’intérêt d’élever la tension sur une ligne électrique?

Aide et solution

m=\dfrac{N_2}{N_1}=6=\dfrac{U_2}{U_1}

donc :

U_2=6 \times 10=60\,V

.
Donc :

I_1=\dfrac{P}{U_1}=\dfrac{36}{10}=3,6\,A

I_2=\dfrac{P}{U_2}=\dfrac{36}{60}=0,6\,A

. On remarque aussi que

\dfrac{I_1}{I_2}=\dfrac{3,6}{0,6}=6=m

.
En élevant la tension on abaisse l’intensité et les pertes en ligne par effet joule (

R\cdot I^2

) sont limitées.

8 - Isolation et résistance thermique

On considère un mur de surface $2\,m^2$ constitué de béton d’épaisseur 20cm doublé avec du plâtre d’épaisseur 5cm.
La température extérieure est $T_{ext}=3^{\circ}C$ et la température intérieure est $T_{int}=19^{\circ}C$ .
On donne les conductivités thermiques : $\lambda_{beton}=1,8\,W.K^{-1}.m^{-1}$ et $\lambda_{platre}=0,25\,W.K^{-1}.m^{-1}$

Calculer la puissance que doit fournir le chauffage pour maintenir constante la valeur de la température intérieure en régime permanent.

Aide et solution

Béton et plâtre sont en série et donc on ajoute les résistances thermiques pour avoir la résistance du mur.

R_{th}=\dfrac{e_{beton}}{\lambda_{beton} \times S} + \dfrac{e_{platre}}{\lambda_{platre} \times S}=\dfrac{0,20}{1,8 \times 2}+\dfrac{0,05}{0,25 \times 2}=0,106\,K.W^{-1}

Le flux thermique perdu est :

\Phi=\dfrac{T_{ext}-T_{int}}{R_{th}}=\dfrac{19-3}{0,106} \approx 151\,W

. Il faut donc que le chauffage fournisse une puissance

P=\Phi

pour compenser les pertes de chaleur et maintenir la valeur de la température intérieure à

19^{\circ}C

9 - Chute d’une boule de bowling

Une boule de bowling, assimilable à un point matériel, de masse $m=4,0\,kg$ , tombe sans vitesse initiale d’une hauteur $h=1,80\,m$ .
Les frottements sont négligés et on prends $g=10\,m.s^{-2}$ .

Calculer :

le travail du poids
la vitesse de la boule lorsqu’elle touche le sol
la durée de la chute
les nouveaux paramètres si cette fois on suppose qu’une force constante de 10N s’oppose à la chute.

Aide et solution

Cadre de l’étude : Référentiel = salle de bowling, système = $\lbrace boule \rbrace$ .

Travail du poids : $W(\vec{P})=m \cdot g \cdot h=4,0 \times 10 \times 1,80=72\,J$
Théorème énergie cinétique TEC : $\dfrac{1}{2} \, m \cdot v^2_B - \dfrac{1}{2} \, m \cdot v^2_A=W(\vec{P})$
or ici $v_A=0$ donc : $\dfrac{1}{2} \, v^2_B=g \cdot h$ d’où : $v_B=\sqrt{2\,g \cdot h}=\sqrt{2\times 10 \times 1,80}=6\,m.s^{-1}=21,6\,km/h$ .
Principe Fondamental de la Dynamique PFD : $m \cdot \vec{a}=\sum \vec{F}_{ext}$ donc ici : $m \cdot \vec{a}=\vec{P}=m \cdot \vec{g}$
On en déduit que : $\vec{a}=\vec{g}$ et donc en projection sur un axe (O,y) vertical ascendant avec O au sol, $a=-g=-10\,m.s^{-2}$
Alors en “primitivant” : $v(t)=-10 \, t+v_0=-10\,t$ car $v_0=0$ et $y(t)=-5\,t^2+y_0=-5\,t^2+1,80$
Lors que la boule est au sol, $y(t)=0$ alors : $t^2=1,80/5=0,36$ et $t=\sqrt{0,36}=0,6\,s$ .
La boule met 0,6s à toucher le sol.
Avec frottements : on trouverait $v_B=\sqrt{2gh-\dfrac{2 \times F_{frott} \times h}{m}}=5,2\,m.s^{-1}=18,7\,km/h$ .
Et la durée de la chute : $a=-g+\dfrac{F_{frott}}{m}=-7,5\,m.s^{-2}$ donc : $v(t)=-7,5\,t$ , $y(t)=-3,75\, t^2+1,80$ et $y(t)=0$ pour $t=0,69\,s$

10 - Frottements de l’air et voiture

Une voiture circule sur une route plane à vitesse constante de 68 km/h. Elle se heurte à un vent de face constant de vitesse 40 km/h. (les autres frottements sont négligés)
Données voiture : $L=4,20\,m$ , $H=1,60\,m$ , $\ell = 1,90\,m$ , $C_x=0,35$ et $\rho_{air}=1,2\,kg/m^3$ .

Quelle puissance développe le moteur de la voiture pour maintenir constante sa vitesse?
Quelle autonomie en km pour une voiture électrique chargée avec 52,0kWh?

Aide et solution

La vitesse relative du vent par rapport à la voiture est $v=68+40=108\,km/h=30\,m.s^{-1}$
La force de frottement fluide contre laquelle le moteur doit lutter est : $F_{frott}=\dfrac{1}{2} \, \rho \cdot C_x \cdot S \cdot v^2=0,5\times 1,2 \times 0,35 \times 1,90 \times 1,6 \times 30^2=575\,N$
Vocabulaire : $C_x$ coefficient de trainée, $S$ maître-couple en $m^2$ .

Comme la vitesse est constante, la force motrice $\vec{F}$ compense exactement la force de frottement $\vec{F}_{frott}$ et donc la puissance à fournir est : $P=F \times v=575 \times 30 =17,3\,kW$ .

La durée de fonctionnement dans ces conditions est

\Delta t= \dfrac{E}{P}=\dfrac{52,0}{17,3}=3,0\,h

soit une distance parcourue

D=v \times \Delta t=68 \times 3,0=204\,km

11 - Mouvement de rotation

Une éolienne de diamètre 12m tourne à 45 tr/min et est entraînée par le vent avec un moment de couple $C=650\,N.m$ . L’éolienne produit 2kW de puissance électrique.

Calculer le rendement $\eta$ de l’éolienne puis la vitesse $v(m/s)$ d’un point en bout de pale.

Aide et solution

Vitesse angulaire :

\Omega=\dfrac{2\pi \cdot N}{60}=4,7\,rad.s^{-1}

donc

P_{meca}=C \times \Omega= 650 \times 4,7=3,06\,kW

.
Donc

\eta=\dfrac{P_{elec}}{P_{meca}}=\dfrac{2}{3,06}=65\%

.
La vitesse en bout de pale est :

v=R \cdot \Omega=6 \times 4,7=28,2\,m.s^{-1} \approx 102\,km/h

12 - Statique des fluides

On considère un réservoir cylindrique de hauteur $H=6\,m$ et de diamètre $D=4\,m$ . Le réservoir est rempli au 2/3 par du fioul domestique de masse volumique $\rho_{fioul}=880\,kg/m^3$ .
On rappelle que : $P_{atm}=1,013.10^5\,Pa$ et $g=10\,N.kg^{-1}$ .

Calculer la masse de fioul, la pression absolue au fond du réservoir et la force en N issue de la surpression due au fioul.

Aide et solution

Volume de fioul :

V= \dfrac{2}{3} \, H \times \pi \times \dfrac{D^2}{4}=50,3\,m^3

.
La masse de fioul est donc :

m= \rho_{fioul} \times V=880 \times \approx 44\,300\,kg

.
La pression absolue au fond du réservoir est :

p_{abs}=P_{atm}+\rho_{fioul} \cdot g \cdot \dfrac{2}{3} \,H=1,013.10^5 + 880 \times 10 \times 4=1,365.10^5\,Pa=1,365\,bar

La force due à la surpression est F telle que :

F=p_{rel} \times S=\rho_{fioul} \times g \times \dfrac{2}{3} \, H \times pi \times \dfrac{D^2}{4}=4,42.10^5\,N

13 - Énergie photonique

Un laser de puissance 2mW émet une couleur rouge à 632nm.
On rappelle que : $h=6,63.10^{-34}\,J.s$ , $1\,eV=1,6.10^{-19}\,J$ .

Déterminer la fréquence $f$ puis l’énergie transportée par un photon de ce laser.

Aide et solution

Calcul de la fréquence :

f=\dfrac{c}{\lambda}=\dfrac{3,00.10^8}{632.10^{-9}}=4,75.10^{14}\,Hz

.
L’énergie d’un photon est donc :

E = h \cdot f = 6,63.10^{-34} \times 4,75.10^{14}=3,15.10^{-19}\,J=1,97\,eV

14 - Changement d’état

Le dégivrage d’un pare-brise de surface $2\,m^2$ couvert uniformément d’une épaisseur $e=1\,mm$ de glace d’eau utilise une résistance $R=0,12\,\Omega$ alimentée en continu par une batterie 12V.

La température extérieure est $-5\,^{\circ}C$ et la pression normale.
On rappelle que : $c_{glace}=2060\,J.kg^{-1}.K^{-1}$ , $L_{fusion}=333\,kJ.kg^{-1}$ , $\rho_{glace}=931\,kg/m^3$ .

Combien de temps faut-il pour dégivrer totalement ce pare-brise?

Aide et solution

Calculons d’abord la masse de glace :

m=e \times S \times \rho_{glace}=0,001 \times 2 \times 931=1,86\,kg

L’énergie pour amener la glace à

0^{\circ}C

E_1=m \times c_{glace} \times (0-(-5))=19,2\,kJ

L’énergie pour faire fondre la glace :

E_2 = m \times L_{fusion}=1,86 \times 333=619,4\,kJ

Pour faire fondre la glace il faut

E=E_1+E_2=638,6\,kJ \approx 639\,kJ

Or la puissance dissipée par effet joule est :

P_J=\dfrac{U^2}{R}=1200\,W

Donc il faut :

\Delta t=\dfrac{E}{P}=\dfrac{639.10^3}{1200}=532\,s=8\,min\,50\,s

15 - Combustion

On brûle $m=2\,g$ de butane $C_4H_{10}$ de PCI 45,7 MJ/kg en combustion complète.
On donne en g/mol : M(H) = 1; M(O) = 16; M(C) = 12 ;

Écrire l’équation chimique de combustion complète puis calculer la masse de dioxyde de carbone produite et l’énergie lbérée.
Quelle solution permettrait d’utiliser le PCS et d’être plus efficace? Donner un exemple.

Aide et solution

Équation : $C_4H_{10} + \dfrac{13}{2} \,O_2 \rightarrow 4\, CO_2 + 5\, H_2O$
Quantité de matière de butane : $n=\dfrac{m}{M}=\dfrac{2}{58}=3,45.10^{-2}\,mol$
L’équation permet de dire que : $n(Co_2)=4 \times n=0,138\,mol$
Donc : $m(CO_2)=n(CO_2) \times M(CO_2)=0,138 \times 44=6,07\,g$ .

L’énergie dégagée par 2g de butane est :

E=m \times PCI=2.10^{-3} \times 45,7.10^6=91,4\,kJ

.
Pour être plus efficace il faudrait récupérer aussi l’énergie de liquéfaction des vapeurs. Ainsi l’efficacité énergétique de la combustion augmenterait comme dans une chaudière à condensation.

16 - pH et réaction acide-base

On ajoute 10mL de soude (NaOH en solution aqueuse : $Na^{+}+HO^{-}$ ) de concentration $c_b=0,02\,mol.l^{-1}$ à 8mL d’acide sulfurique $H_2SO_4$ ( $2H_3O^{+}+SO^{2-}_4$ en solution) de concentration $c_a=0,015\,mol.L^{-1}$ .

Calculer le pH avant ajout de soude.
Identifier les ions réactifs puis écrire l’équation de réaction acide-base. (ne pas tenir compte des ions spectateurs)
Calculer le nouveau pH après l’ajout de soude.

Aide et solution

Avant ajout : $\left[H_3O^{+} \right]=2 \times c_a=0,03\,mol.L^{-1}$ donc : $pH=-log \left[H_3O^{+} \right]=1,52$

Réaction acide-base : $H_3O^{+} + HO^{-} \rightarrow 2 \, H_2O$

Estimation des quantités de matière :

n_a=\left[H_3O^{+} \right] \cdot V_a=0,03 \times 8.10^{-3}=2,4.10^{-4}\,mol

n_b=c_b \times V_b=0,02 \times 0,010=2,0.10^{4}\,mol

.
Il reste donc :

n=n_a-n_b=0,4.10^{-4}\,mol

H_3O^{+}

dans 18mL de solution.
La nouvelle concentration effective est :

\left[H_3O^{+} \right]=\dfrac{n}{V}=\dfrac{0,4.10^{-4}}{0,018}=2,22.10^{-3}\,mol.L^{-1}

et donc le nouveau pH est 2,66.

17 - Son et musique

L’enregistrement du son émis par un instrument de musique jouant une seule note est (unités en V et ms) :

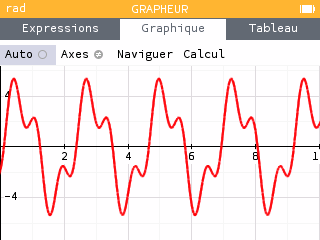
énergie

Déterminer la note jouée par l’instrument. S’agit-il d’un son pur ou complexe?
De quelle famille d’onde fait partie le son? Quelles sont ses les principales propriétés de ce type d’onde?.
Décrire l’allure du spectre en amplitude (unités V et Hz) en utilisant le vocabulaire adapté.
énergie

Aide et solution

Il y a environ 3,5 périodes en 8ms. Donc

T=8/3,5=2,28\,ms

. Donc

f=\dfrac{1}{T}=439\,Hz \approx 440\,Hz

. Il s’agit de la note LA de l’octave 3.
Le son est complexe car non sinusoïdal. Il est périodique donc peut être décomposé en somme de fonctions sinusoïdales (Théorème de Fourier).
Le son est une onde mécanique qui a besoin de matière pour se propager à environ 340 m/s dans l'air sec à 20°C.
Le spectre est composé de deux pics, le premier à 440Hz se nomme le fondamental dont l’amplitude est 4V et le suivant est l’harmonique de rang 3 dont l’amplitude vaut 1,8V.

18 - Niveau et intensité sonores

Quatre smartphone identiques et réglés de la même façon émettent chacun une sonnerie d’intensité $I=1,0.10^{-4}\,W/m^2$ .

Déterminer en dB le niveau sonore $L$ mesuré.
Qu’affiche le sonomètre si on éteint 2 smartphones? Puis si on ne laisse qu’un smartphone sonner?

Aide et solution

L=10 \,log \left( \dfrac{4 \times I}{I_0} \right)=10 \,log(4,0.10^8)=86\,dB

Si on éteint 2 smartphones, alors

L=10 \,log \left( \dfrac{2\,I}{I_0} \right)=83\,dB

On retrouve le résultat connu, chaque fois qu’on diminue par 2 l’intensité sonore, on retire 3dB.
Si on éteint encore un smartphone, on doit perdre encore 3dB soit

L=80\,dB

. On vérifie par un calcul direct, si un seul smartphone sonne :

L=10 \,log \left( \dfrac{1 \times I}{I_0} \right)=10 \, log(1,0.10^8)=80\,dB

.
Si plusieurs sources, on peut ajouter les $\mathbf{I(W/m^2)}$ mais PAS les L(dB) !

19 - Taille d’une antenne

Un smartphone utilise la bande 4G LTE à 750 MHz pour communiquer avec le réseau mobile.

Calculer la taille de l’antenne demi-onde nécessaire à la transmission.
Dans quelle catégorie classer l’onde utilisée pour la transmission? A-t-elle besoin de matière pour se propager?

Aide et solution

f=7,50.10^8\,Hz

donc

\lambda=\dfrac{c}{f}=\dfrac{3,00.10^8}{7,50.10^8}=0,4\,m

.
Il faut donc 0,2m soit 20cm pour assurer la bonne transmission avec une antenne demi-onde.
L’onde est électromagnétique (hyperfréquence, onde radio) et n’a pas besoin de matière pour se propager.

20 - Fission nucléaire

Dans un réacteur a lieu la réaction en chaîne suivante : $^1_0n \, + \, ^{235}_{\,92}U \, \rightarrow \, ^{140}_{\,56}Ba \, + \, ^{93}_{...}Kr \, + \, ...\, ^{1}_0n$
Données : $1\,u=931,49403\,MeV/c^2$ ; $m(^{235}U)=235,04393\,u$ ; $m(^{140}Ba)=139,910605\,u$ ; $m(^{93}Kr)=92,93127\,u$ ; $m(^1_0n)=1,00866\,u$
$1\,eV=1,602177.10^{-19}\,J$ ; $c=299\,792\,458\,m/s$ et $1g$ d’uranium 235 contient $2,562.10^{21}$ noyaux.

Équilibrer l’équation de réaction puis déterminer l’énergie produite par la réaction d’1g d’uranium 235.

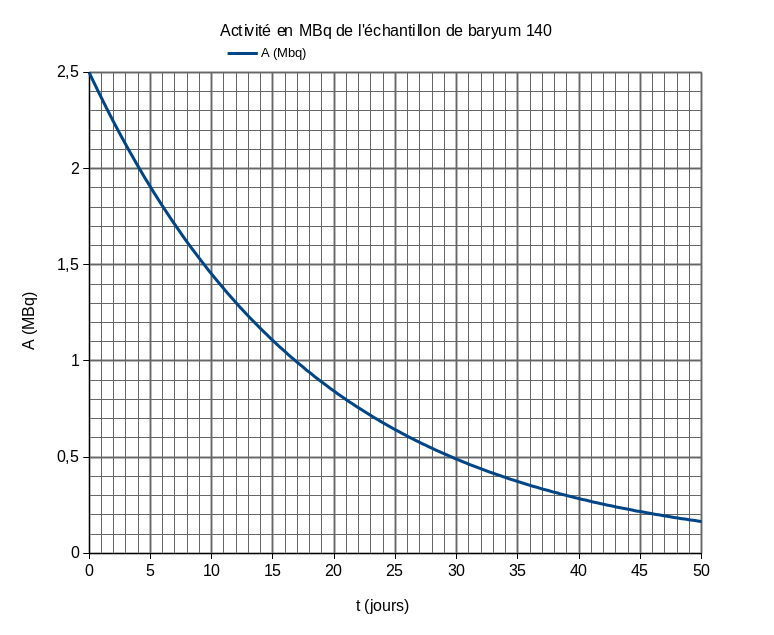
panneau

Déterminer l’activité initiale de l’échantillon de baryum 140 produit par la fission et qui se désintègre en lanthane 140 ainsi que sa demi-vie $T_{1/2}$ .

Aide et solution

$^1_0n \, + \, ^{235}_{\,92}U \, \rightarrow \, ^{140}_{\,56}Ba \, + \, ^{93}_{36}Kr \, + \, 3\, ^{1}_0n$

On calcule la variation de masse : $\Delta m=m(^{140}Ba)+m(^{93}Kr)+2 \times m(^1_0n) - m(^{235}U)=-0,18474\,u = -172,079\,MeV/c^2$
La variation de masse est négative (il y a donc défaut de masse) donc le système perd de la masse qui est transformée en énergie.
Cette énergie est libérée et se calcule par $E=\vert \Delta m \vert \cdot c^2$ . On en déduit qu’un noyau d’uranium libère $E=172,079\,MeV=2,76.10^{-11}\,J$
Donc pour 1g, l'énergie libérée est : $E_{1g}=2,562.10^{21} \times 2,76.10^{-11}=70,6.10^9\,J=70,6\,GJ$ !

Remarque : Si les masses étaient données et kg
Calcul de $\Delta m$ en kg $\rightarrow$ calcul en J de $E=\vert \Delta m \vert \cdot c^2$ (besoin ici de la valeur de c) $\rightarrow$ conversion éventuelle en MeV.

L’activité initiale se lit pour t = 0 soit $A_0=2,5\,MBq$ . La demi-vie est atteinte pour $A=\dfrac{A_0}{2}=1,25\,j$ soit $T_{1/2} \approx 13\,j$ . En théorie, la demi-vie ou période du baryum 140 est 12,75 jours.

21 - Panneau photovoltaïque

Un panneau solaire est composé de 72 cellules de surface $S_c=5.10^{-4}\,m^2$ chacune.
Le panneau est exposé à une irradiance $I_r=910\,W.m^{-2}$ et une étude expérimentale permet de tracer ses caractéristiques (courbe bleue $I=f(U)$ , courbe rouge $P=g(U)$ , axes bas U(V), gauche I(A), droite P(W)) :

panneau

Déterminer l’intensité du courant de court-circuit $I_{CC}$ et la tension à vide $U_0$ du panneau puis le rendement maximal $\eta$ de ce panneau solaire et la nature du silicium utilisé.

Aide et solution

L’intensité $I_{CC}$ est l’ordonnée à l’origine de la courbe bleue et donc $I_{CC} \approx 0,34\,A$ , la tension à vide se lit sur l’axe horizontale et $U_0 \approx 21\,V$ .
La surface totale $S=72 \times S_c= 72 \times 5.10^{-4}=0,036\,m^2$ .
La puissance rayonnée reçue est : $P_{ray} = I_r \times S=910 \times 0,036 = 32,8\,W$ .
La courbe rouge montre que la puissance maximale électrique produite est $P_{elec} \approx 4,7\,W$ (on parle aussi de puissance crête en Wc) donc le rendement maximal est : $\eta=\dfrac{P_{elec}}{P_{ray}}=\dfrac{4,7}{32,8}=14,3\%$
Entre 10 et 15%, il s’agit souvent de silicium polycristallin. Si le rendement est meilleur c’est du monocristallin (moins bon ça peut être de l’amorphe).

22 - Incertitude de mesure

On mesure une distance D de 2 façons : avec un réglet gradué au mm et avec un émetteur-récepteur à ultrasons (US).

Au réglet : D = 153 mm avec une étendue 2a = 1 mm
Avec le radar US avec c_us = 340 m/s, effectue 10 mesures de la durée dt en µs

mesure	1	2	3	4	5	6	7	8	9	10
dt(µs)	898	902	901	903	896	897	898	899	904	902

Pour la mesure avec le réglet, calculer l'incertitude-type $u (D) = \frac{a}{\sqrt{3}}$ puis exprimer un encadrement de D en mm.
Calculer la ligne correspondant à D puis calculer l'écart-type échantillon (incertitude), la moyenne et la médiane des mesures de D avec le radar puis donner un encadrement du résultat de mesure de D en mm.

Aide et solution

Avec le réglet : u(D)=0,29mm et donc : 152,71 ≤ D ≤ 153,29 mm.
Avec le radar US : u(D)=0,47mm et la valeur la plus probable est 153 mm telle que D = 153 ±0,47 mm